Deep Learning/Diffusion

Denoising Diffusion Probabilistic Model

728x90

1. 배경 지식

1.1. Variational AutoEncoder

Auto Encoder 요약

1. 개념어떠한 데이터 입력이 들어왔을 때, 해당 입력을 압축 시켜 latent vector로 만든 후, 해당 embedding vector를 다시 본래의 입력 데이터 형태로 복원 하는 신경망 2. 구조인코더와 디코더로 이루

alstn59v.tistory.com

1.2. KL Divergence

KL Divergence

0. 들어가기에 앞서본 게시글은 쿨백-라이블러 발산(Kullback–Leibler divergence, KLD)에 대해 쉽게 이해할 수 있도록 최대한 간략하게 작성한 글입니다.더욱 자세한 내용을 알고싶다면, 아래의 참고

alstn59v.tistory.com

1.3. Markov Chain

Markov Chain Monte Carlo - 공돌이의 수학정리노트 (Angelo's Math Notes)

angeloyeo.github.io

1.4. U-Net

U-Net: Convolutional Networks for Biomedical Image Segmentation

0. 시작하기에 앞서본 게시물은 아래 참고링크의 게시글을 매우 적극적으로 활용하였으므로, 원 저작자에게 감사의 뜻을 남깁니다. 1. 개념U-Net은 오토인코더(autoencoder)와 같이 데이터의 차원을

alstn59v.tistory.com

2. 물리학에서의 Diffusion

사전적 의미
- 액체나 기체에 다른 물질이 섞이고, 그것이 조금씩 번져가다가 마지막에는 일률적인 농도로 바뀌는 현상 [위키백과]
- 확산은 물질이 원자나 분자의 무질서한 열운동을 통해 농도(concentration)가 높은 영역에서 낮은 영역으로 평균적으로 이동하는 것 [네이버 지식백과]
아래 그림에서 연기가 퍼지는 과정에서의 밀도는 매우 noisy 하기 때문에, 알아내는 것이 매우 어려움
- 그러나, 시간이 지나면 지날수록 연기는 어느 지점에서나 비슷한 밀도로 고르게 분포하게 될 것임
- 또한 매우 작은 time step에서의 확산 과정은 gaussian distribution 안에서 이루어질 것이라고 볼 수 있음

3. 딥러닝에서의 Intuition

물리학의 확산에서 매우 작은 time step에서 이루어지는 과정이 gaussian distribution 안에서 이루어진다면, 이 역과정 또한 gaussian distribution 안에서 이루어질 것이고, 이는 학습할 수 있음
- 즉, 매 time step의 distribution을 학습한다면 위의 그림에서 처음 혹은 특정 시간대의 연기의 밀도도 구할 수 있을 것임

4. Denoising Diffusion Models

noise에서 깔끔한 이미지를 생성하는 과정을 학습하는 모델을 Diffusion Model 이라하며, 이를 위해 이미지에 noise를 입히는 과정과 noise에서 이미지로 만드는 과정으로 이루어짐
- forward diffusion process : 이미지에 지속적으로 조금씩 noise를 더해서, 최종적으로 gaussaian noise map을 만드는 과정
  - 위의 연기가 확산되는 과정에 해당하며, 매우 쉬움
- reverse denoising process : noise에서 이미지를 생성하는 과정

4.1. Forward Diffusion Process

이미지를 gaussian kernel에 계속하여 통과시킨 것으로 볼 수 있음
원본 이미지를 \( \mathbf{x}_{0} \), noise 상태를 \( \mathbf{x}_{T} \)로 정의
- 즉, \( \mathbf{x}_{t} \)에서 \( t \)가 커질수록 noise에 가까우며, \( \mathbf{x}_{t} \)는 아래와 같이 정의할 수 있음
  - \( q(\mathbf{x}_{t}|\mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_{t}; \sqrt{1-\beta_{t}}\mathbf{x}_{t-1}, \beta_{t}\mathbf{I}) \)
    - \( q(\mathbf{x}_{t}|\mathbf{x}_{t-1}) \)는 현재 단계의 이미지 \( \mathbf{x}_{t} \)가 이전 단계의 이미지 \( \mathbf{x}_{t-1} \)에 대해 갖는 분포를 뜻하며, 매우 작은 time step이기 때문에 gaussian distribution을 따름
    - \( \mathcal{N}(\mathbf{x}_{t}; \sqrt{1-\beta_{t}}\mathbf{x}_{t-1}, \beta_{t}\mathbf{I}) \)는 \( \sqrt{1-\beta_{t}}\mathbf{x}_{t-1} \)을 평균, \( \beta_{t}\mathbf{I} \)을 분산으로 하는 normal distribution
    - \( \beta_{t} \)는 매우 작은 값으로 보통 0.000x 정도의 값을 사용
    - 즉, \( \sqrt{1-\beta_{t}}\mathbf{x}_{t-1} \) 부분은 이전 단계의 값을 약간 감소시키는 것을 뜻하며, \( \beta_{t}\mathbf{I} \) 부분은 nosie를 조금 더하는 것을 뜻하며, \( \beta_{t} \)가 커질수록 noise의 양이 많아짐
  - 위의 식은 joint distribution을 이용하여 아래와 같이 작성할 수 있음
    - \( q(\mathbf{x}_{1:T}|\mathbf{x}_{0}) = \prod_{t=1}^{T}{q(\mathbf{x}_{t}|\mathbf{x}_{t-1})} \)

4.1.1. Diffusion Kernel

매 time step마다 이미지에 noise를 조금씩 더하지 말고 특정 time step \( t \)에 해당하는 결과로 한 번에 갈 수 있는 noise를 더해보자는게 DDPM의 핵심 idea
- \( \text{Define } \overline{\alpha}_{t} = \prod_{s=1}^{t}{(1-\beta_{s})} \Rightarrow q(\mathbf{x}_{t}|\mathbf{x}_{0}) = \mathcal{N}(\mathbf{x}_{t}; \sqrt{\overline{\alpha}_{t}}\mathbf{x}_{0}, (1-\overline{\alpha}_{t})\mathbf{I}) \)
  - \( \beta_{t} \) values schedule (i.e., the noise schedule) is designed such that \( \alpha_{T} \rightarrow 0 \) and \( q(\mathbf{x}_{T}|\mathbf{x}_{0}) \approx \mathcal{N}(\mathbf{x}_{T}; 0, \mathbf{I}) \)
    - \( q(\mathbf{x}_{T}|\mathbf{x}_{0}) \)는 최종 샘플링, \( \mathcal{N}(\mathbf{x}_{T}; 0, \mathbf{I}) \)는 완벽한 gaussian noise 상태
- \( \text{For sampling: } \mathbf{x}_{t} = \sqrt{\overline{\alpha}_{t}}\mathbf{x}_{0} + \epsilon \sqrt{1-\overline{\alpha}_{t}} \text{ where } \epsilon \sim \mathcal{N}(0, \mathbf{I}) \)
  - \( \epsilon \sim \mathcal{N}(0, \mathbf{I}) \)은 랜덤한 noise
이 과정은 수학적으로 증명가능(gaussian noise의 특성 상, 누적하다보면 큰 gaussian noise를 더한 것과 같음이 증명 됨)하며, 본 게시물에서 증명 과정은 생략함

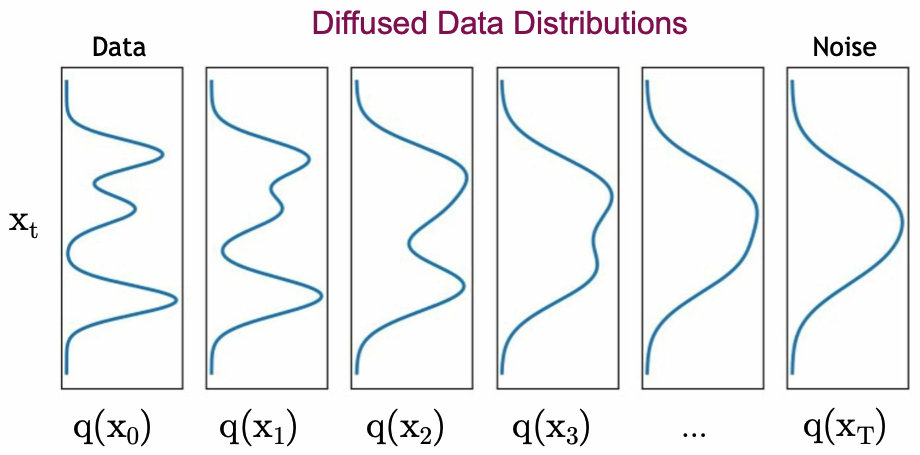
\( q(\mathbf{x}_{t}) \)는 아래와 같이 정의할 수 있음
- \( q(\mathbf{x}_{t}) = \int{q(\mathbf{x}_{0},\mathbf{x}_{t})d\mathbf{x}_{0}} = \int{q(\mathbf{x}_{0})q(\mathbf{x}_{t}|\mathbf{x}_{0})d\mathbf{x}_{0}} \)
  - \( q(\mathbf{x}_{t}) \)는 diffused data distribution, \( q(\mathbf{x}_{0},\mathbf{x}_{t}) \)는 joint distribution, \( q(\mathbf{x}_{0}) \)는 input data distribution, \( q(\mathbf{x}_{t}|\mathbf{x}_{0}) \)는 diffusion kernel
- input data와 diffusion kernel을 결합하는 방식으로, \( \mathbf{x}_{0} \)을 먼저 샘플링하고, 이를 이용해 \( q(\mathbf{x}_{t} | \mathbf{x}_{0}) \)에서 다시 샘플링 하는것과 같음
  - 즉, 복잡한 확률분포 \( q(\mathbf{x}_{t}) \)에서 \( \mathbf{x}_{t} \)를 샘플링하는 대신 두 단계를 거쳐서 접근

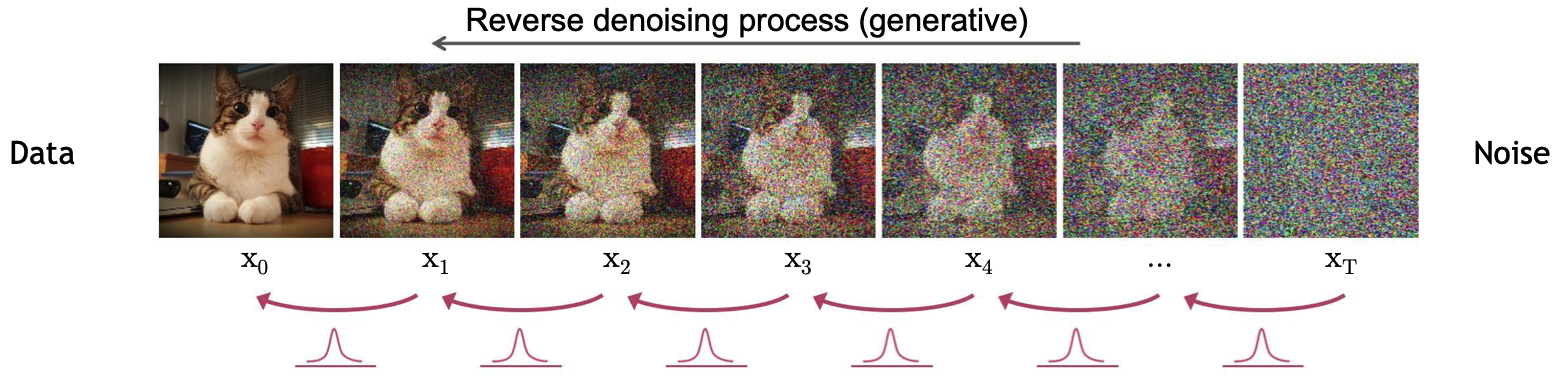
4.2. Reverse Denoising Process

noise를 샘플링
- \( \mathbf{x}_{T} \sim \mathcal{N}(\mathbf{x}_{T}; 0, \mathbf{I}) \)
noise → noise가 덜 더해진 조건부 확률을 알면 \( \mathbf{x}_{t-1} \)를 샘플링
- \( \mathbf{x}_{t-1} \sim q(\mathbf{x}_{t-1} | \mathbf{x}_{t}) \)
  - \( q(\mathbf{x}_{t-1} | \mathbf{x}_{t}) \)는 true denoising distribution

일반적으로 \( q(\mathbf{x}_{t-1} | \mathbf{x}_{t}) \propto q(\mathbf{x}_{t-1}) q(\mathbf{x}_{t} | \mathbf{x}_{t-1}) \)은 intractable 하므로 모델 학습을 통해 다룸
- 그러나 각 forward diffusion step에서 \( \beta_{t} \)가 굉장히 작다면, normal distribution을 활용하여 \( q(\mathbf{x}_{t-1} | \mathbf{x}_{t}) \)를 근사할 수는 있음
  - 역변환도 정규분포를 따르므로 분포의 평균과 표준편차만 구하면 됨
\( T \) step 동안 forward process와 reverse process는 아래와 같이 정의
- forward process : \( p(\mathbf{x}_{T}) = \mathcal{N}(\mathbf{x}_{T}; 0, \mathbf{I}) \)
- reverse process : \( p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t}) = \mathcal{N}(\mathbf{x}_{t-1}; \mu_{\theta}(\mathbf{x}_{t}, t), \sigma_{t}^{2}\mathbf{I}) \Rightarrow p_{\theta}(\mathbf{x}_{0:T}) = p(\mathbf{x}_{T}) \prod_{t=1}^{T}{p_{\theta}(\mathbf{x}_{t-1} | \mathbf{x}_{t})} \)
  - 구하고자 하는 distribution을 추정하기 위해 gaussian distribution을 따른다는 것은 알고있으므로, 평균값인 \( \mu_{\theta}(\mathbf{x}_{t}, t) \) 부분을 파라미터화 하여 U-Net, Denoising AutoEncoder 등을 사용하여 네트워크를 통해 학습

5. Learning Denoising Model

variational upper bound를 이용하여 학습
- \( \mathbb{E}_{q(\mathbf{x}_{0})}\left[-\log{p_{\theta}(\mathbf{x}_{0})}\right] \leq \mathbb{E}_{q(\mathbf{x}_{0}) q(\mathbf{x}_{1:T} | \mathbf{x}_{0})} \left[-\log{\frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} | \mathbf{x_{0}})}}\right] := L \)
  - \( \mathbb{E}_{q(\mathbf{x}_{0})}\left[-\log{p_{\theta}(\mathbf{x}_{0})}\right] \) 부분을 직접 구할수는 없더라도 lower bound는 알 수 있으므로, \( \mathbb{E}_{q(\mathbf{x}_{0}) q(\mathbf{x}_{1:T} | \mathbf{x}_{0})} \left[-\log{\frac{p_{\theta}(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T} | \mathbf{x_{0}})}}\right] \) 부분을 최적화 하면 됨
따라서 모델의 loss는 아래와 같이 정의할 수 있음
- \( L = \mathbb{E}_q \bigg[ \underbrace{D_{KL} (q(x_T | x_0) \; || \; p(x_T))}_{L_T} + \sum_{t>1} \underbrace{D_{KL} (q(x_{t-1} | x_t , x_0) \; || \; p_\theta (x_{t-1} | x_t))}_{L_{t-1}} \underbrace{- \log p_\theta (x_0 | x_1)}_{L_0} \bigg] \)
  - \( L_{T} \)
    - regularization loss에 해당하며, noise의 더한 정도를 나타내는 \( \beta \)가 고정되어있기 때문에 학습에 영향을 미치지 않음
    - \( q(x_T | x_0) \)와 \( p(x_T) \)는 모두 \( \mathcal{N}(0, 1) \)인 gaussian distribution으로 동일하므로, 계산 결과가 0임
  - \( L_{t-1} \)
    - denoising process loss에 해당하며, diffusion model의 역과정이 학습된 역과정 모델 \( p_{\theta} \)와 유사한가를 비교하는 역할
    - \( q(x_{t-1} | x_t , x_0) \)는 noise가 첨가된 데이터 \( \mathbf{x}_{t} \)와 원본 데이터 \( \mathbf{x}_{0} \)를 알 때, 이 noise를 어떻게 제거할지에 대한 확률분포로, 알고 있는 분포로 tractable함
      - \( q(x_{t-1} | x_t , x_0) = \mathcal{N}(\mathbf{x}_{t-1} ; \tilde{\mu}_{t}(\mathbf{x}_{t}, \mathbf{x}_{0}), \tilde{\beta}_{t}\mathbf{I}) \)
        
        \( \text{where } \tilde{\mu}_{t} (x_t, x_0) := \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} x_0 + \frac{\sqrt{1-\beta_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} x_t \text{ and } \tilde{\beta}_{t} := \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \beta_{t} \)
        
        즉, \( \mathbf{x}_{0} \)과 \( \mathbf{x}_{t} \)를 알면 적당히 스케일링하여 근사할 수 있음
    - \( p_\theta (x_{t-1} | x_t) \)는 noise가 첨가된 데이터 \( \mathbf{x}_{t} \)에서 이전 시점 데이터 \( \mathbf{x}_{t-1} \)을 추정하는 모델이 학습한 확률분포
  - \( L_{0} \)
    - reconstruction loss에 해당
    - 원본 데이터 \( \mathbf{x}_{0} \)와 1 step 후의 데이터인 \( \mathbf{x}_{1} \)에 대해 조건부 분포를 계산하는 값이므로, 두 분포가 거의 비슷하여 영향력이 매우 적기 때문에 무시 가능
  - 즉, 실제로 모델이 학습하는 term은 \( L_{t-1} \) 임

5.1. Parameterizing the Denoising Model

\( q(x_{t-1} | x_t , x_0) \)와 \(p_\theta (x_{t-1} | x_t) \)를 모두 normal distribution으로 가정했으므로, 두 분포사이의 KL-Divergence를 gaussian distribution 사이의 KL-Divergence 공식으로 표현할 수 있음
- \( L_{t-1} = D_{KL} (q(x_{t-1} | x_t , x_0) \; || \; p_\theta (x_{t-1} | x_t)) = \mathbb{E}_{q} \left[ \frac{1}{2\sigma_{t}^{2}} \left\| \tilde{\mu}_{t}(x_t , x_0)-\mu_{\theta}(x_t , t) \right\|^{2} \right] + C \)
  - \( \tilde{\mu}_{t}(x_t , x_0) = \frac{1}{\sqrt{1-\beta_{t}}} \left( \mathbf{x}_{t} - \frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon \right) \)
  - \( \mu_{\theta}(x_t , t) = \frac{1}{\sqrt{1-\beta_{t}}} \left( \mathbf{x}_{t} - \frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon_{\theta} (\mathbf{x}_{t}, t) \right) \)
    - \( \epsilon_{\theta} (\mathbf{x}_{t}, t) \)로 표현된 noise prediction network를 통해서 우리가 알고싶어하는 gaussian model의 평균을 예측할 수 있음
    - 즉, noise prediction만 하면 평균을 예측할 수 있음
4.1.1. 에서 조금씩 noise를 더하는 과정을 한 번에 sampling하여 \( \mathbf{x}_{t} \)를 정의했는데, 해당 식을 위의 식에 대입하면 \( L_{t-1} \)를 아래와 같이 정리할 수 있음
- \( L_{t-1} = \mathbb{E}_{\mathbf{x}_0 \sim q(\mathbf{x}_0), \epsilon \sim \mathcal{N}(0, \mathbf{I})} \bigg[ \underbrace{\frac{\beta_t^2}{2\sigma_t^2 \alpha_t (1-\bar{\alpha}_t)}}_{\lambda_{t}} \| \epsilon - \epsilon_\theta (\underbrace{\sqrt{\vphantom{1} \bar{\alpha}_t} + \sqrt{1-\bar{\alpha}_t} \epsilon}_{\mathbf{x}_{t}}, t) \|^2 \bigg] + C \)
  - DDPM 논문에서는 \( \lambda_{t} \)를 1로 설정하는게 좋다고 함
    - 그러므로 위의 식은 최종적으로 아래와 같이 정리할 수 있음
      - \( L_{\text{simple}} = \mathbb{E}_{\mathbf{x}_0 \sim q(\mathbf{x}_0), \epsilon \sim \mathcal{N}(0, \mathbf{I}), t \sim \mathcal{U}(1, T)} \bigg[ \| \epsilon - \epsilon_\theta (\underbrace{\sqrt{\vphantom{1} \bar{\alpha}_t} + \sqrt{1-\bar{\alpha}_t} \epsilon}_{\mathbf{x}_{t}}, t) \|^2 \bigg] + C \)

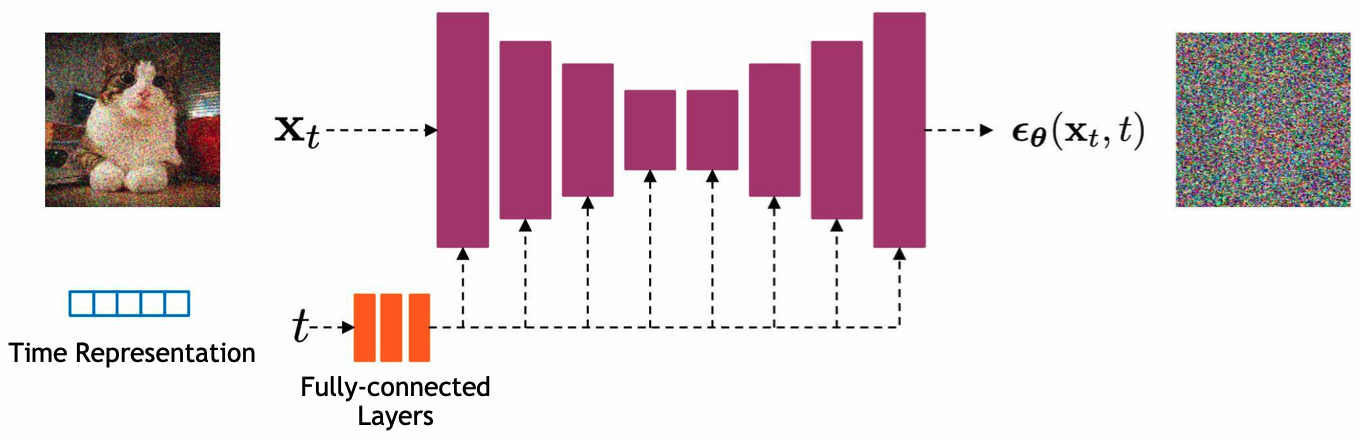
6. Network Architectures

U-Net에 \( \mathbf{x}_{t} \)와 \( t \)가 입력으로 들어가면 어떤 noise가 더해진 것인지 prediction을 하고, 이를 이용하여 \( \mathbf{x}_{t-1} \)을 생성하는 구조로 되어있으며, U-Net 구조 안에 self-attention과 group normalization 등이 포함되어 있음
- 최종적으로는 \( \mathbf{x}_{0} \)를 얻음
- Network Training Step
  - dataset에서 이미지를, gaussian distribution에서 같은 크기의 noise를 샘플
  - uniform distribution에서 학습할 diffusion time을 샘플, diffusion schedule에 따라서 noise를 더할 강도를 계산
  - noise가 더해진 이미지 생성
  - noise가 더해진 이미지와 diffusion time을 입력받아 noise를 예측하도록 DDPM model을 학습

6.1. Content-Detail Tradeoff

초기 단계
- noise에서 시작하기 때문에 처음에는 low-frequency content를 만들며, 어떤 data를 생성할지 정해지는 단계
후반 단계
- data의 detail한 정보를 추가하여 high-frequency content를 만드는 단계

7. Summary

Training Algorithm
- 실제 데이터 \( \mathbf{x}_{0} \)에 noise를 추가하여 noise가 더해진 데이터 \( \mathbf{x}_{t} \)를 생성하고, 모델이 예측한 noise와 실제 noise간의 차이를 최소화하도록 파라미터를 업데이트

Sampling Algorithm
- 초기 노이즈 상태 \( \mathbf{x}_{T} \)에서 시작하여, 모든 time step을 반복하면서 현재 상태에서 예측된 noise를 제거하고, 모델의 불확실성과 다양한 샘플을 생성하기 위해서 noise를 추가하여 초기상태 \( \mathbf{x}_{0} \)을 반환