Towers of Hanoi

Towers of Hanoi in C

코드 소개

• C언어를 이용하여 n개의 원반이 있는 하노이의 탑 문제에서 원반의 이동횟수를 구하는 프로그램이다.

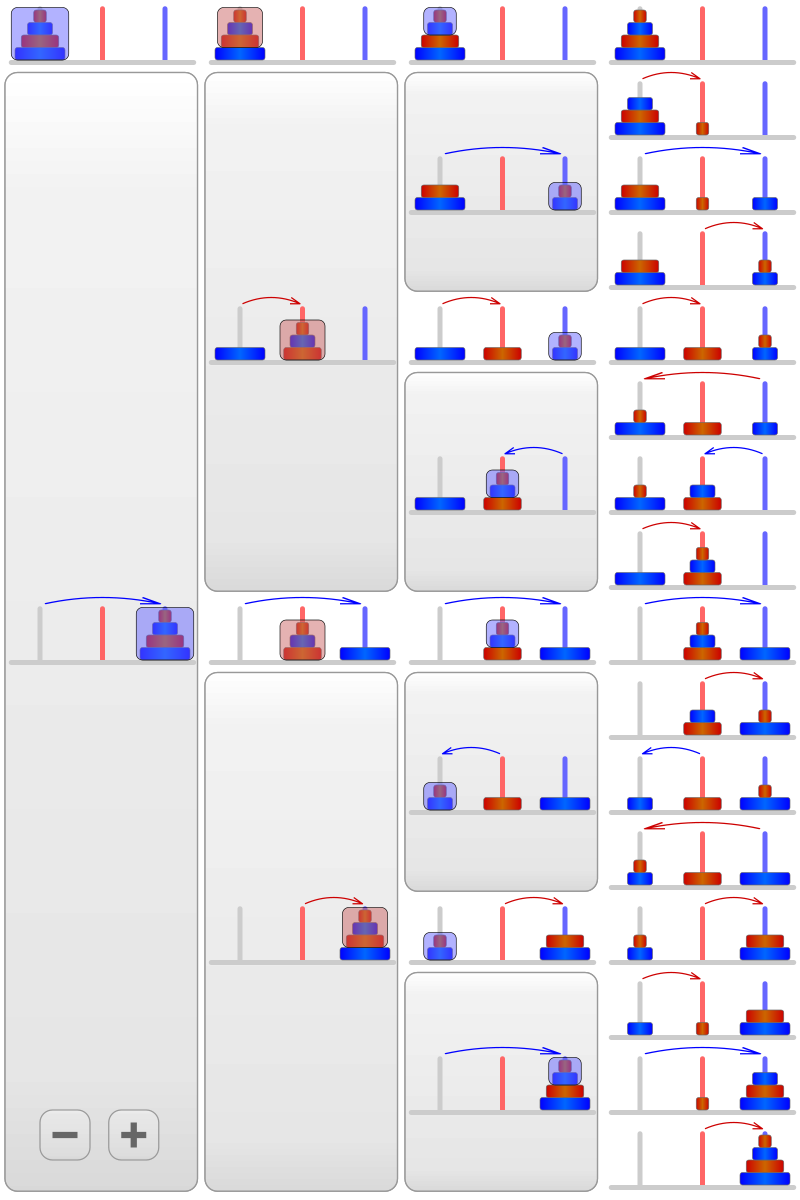
하노이의 탑

• 1883년 프랑스 수학자 루카스(Lucas)에 의해 고안된 문제인데, 가운데 기둥을 이용해서 왼쪽 기둥에 놓인 크기가 다른 n개의 원판을 오른쪽 기둥으로 옮기는 문제였다. 이때 원판은 한번에 한 개씩만 옮길 수 있으며, 작은 원판 위에 큰 원판이 놓일 수 없다는 조건이 따른다.
• 하노이의 탑에서 원판 옮기는 과정

코드

//============================================================================
// Name        : Towers_of_Hanoi.c
// Author      : Minsu Jo
// Created on  : 2016. 6. 11.
// Description : Ansi-style
//============================================================================

/* 재귀함수를 이용한 하노이의 탑 이동 횟수 구하기 */

#include <stdio.h>

void hanoiTower(int n, char from, char temp, char to); // 이동 횟수 계산 함수
int count; // 이동 횟수

int main()
{
    int n; // 이동시킬 원판의 개수

    setvbuf(stdout, NULL, _IONBF, 0);
    setvbuf(stderr, NULL, _IONBF, 0);

    printf("Please enter the number of disc : ");
    scanf("%d", &n);

    hanoiTower(n, 'A', 'B', 'C'); // 이동 횟수 계산 함수에 n을 넣어서 호출

    printf("Move : %d times.", count);

    return 0;
}

void hanoiTower(int n, char from, char temp, char to)
{ // 하노이의 탑 점화식 => A(n) = 2(A(n-1)) + 1
    if(n == 1) // 원판이 하나일 경우
    {
        printf("Move  [disc %d]  from <%c>  to  <%c>.\n", n, from, to);
        count++;
    }
    else // 원판이 하나가 아닐 경우
    {
        hanoiTower(n-1, from, to, temp);
        printf("Move  [disc %d]  from <%c>  to  <%c>.\n", n, from, to);
        count++;
        hanoiTower(n-1, temp, from, to);
    }
}

입력 데이터

5

실행결과

Move  [disc 1]  from <A>  to  <C>.
Move  [disc 2]  from <A>  to  <B>.
Move  [disc 1]  from <C>  to  <B>.
Move  [disc 3]  from <A>  to  <C>.
Move  [disc 1]  from <B>  to  <A>.
Move  [disc 2]  from <B>  to  <C>.
Move  [disc 1]  from <A>  to  <C>.
Move  [disc 4]  from <A>  to  <B>.
Move  [disc 1]  from <C>  to  <B>.
Move  [disc 2]  from <C>  to  <A>.
Move  [disc 1]  from <B>  to  <A>.
Move  [disc 3]  from <C>  to  <B>.
Move  [disc 1]  from <A>  to  <C>.
Move  [disc 2]  from <A>  to  <B>.
Move  [disc 1]  from <C>  to  <B>.
Move  [disc 5]  from <A>  to  <C>.
Move  [disc 1]  from <B>  to  <A>.
Move  [disc 2]  from <B>  to  <C>.
Move  [disc 1]  from <A>  to  <C>.
Move  [disc 3]  from <B>  to  <A>.
Move  [disc 1]  from <C>  to  <B>.
Move  [disc 2]  from <C>  to  <A>.
Move  [disc 1]  from <B>  to  <A>.
Move  [disc 4]  from <B>  to  <C>.
Move  [disc 1]  from <A>  to  <C>.
Move  [disc 2]  from <A>  to  <B>.
Move  [disc 1]  from <C>  to  <B>.
Move  [disc 3]  from <A>  to  <C>.
Move  [disc 1]  from <B>  to  <A>.
Move  [disc 2]  from <B>  to  <C>.
Move  [disc 1]  from <A>  to  <C>.
Move : 31 times.